「有意差」って何？～偶然の産物、誤差ではないことの保証

回答：意味の有る差、ということ

　「有意差」とは、偶然や誤差で生じた差ではない、「意味の有る差」のことを意味します。

　見た目のグラフや数字がどれほど大きく違っていようと、「有意差」がついていなければ、それは統計学的には差がないことになります。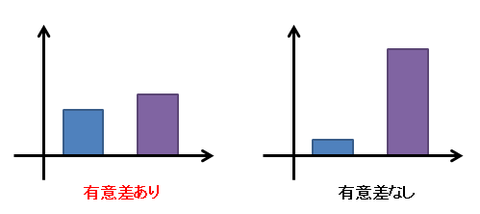

　平たく言うと、「有意差」のつかなかった差は、単なる偶然や誤差で生じた意味のない差だと解釈されます。

詳しい回答①：誰もが納得する、一定の判断基準が必要

　薬を飲んで血圧が下がった場合、それは「確実に薬の効果」によるものなのか、あるいは単なる「偶然」や「誤差」でしかないのか、それを判断する必要があります。
　しかし、この判断は主観的に行えるものではありません。そのため、統計を使った一定の判断基準を利用します。
　

誰の目にも明らかな偶然

　例えば、サイコロを3回振ったとします。このとき、3回とも「6」の目が出たとします。
　この結果を見て、「このサイコロは、「6」の目を出す不思議なサイコロである！」と結論付けることは、妥当でしょうか。

　恐らく、ほとんどの人が「いや、単なる偶然だろう」と言うはずです。次にサイコロを振ったら違う数字が出るかもしれない、という可能性があるからです。

誰の目にも明らかな必然

　では、サイコロを100億回振ったとします。このとき、「6」の目が99億9999万9998回出て、あとは「1」と「3」の目が1回ずつ出たとします。
　この結果を見て、「このサイコロは、「6」の目を出す不思議なサイコロである！」と結論付けることは、妥当でしょうか。

　恐らく、ほとんどの人が頷くはずです。次からサイコロを振っても、ほとんど確実に「6」が出続けるからです。

偶然か必然か、微妙なもの

　それでは、サイコロを100回振ったとします。このとき、「6」の目が25回出たとします。

　サイコロの目は6種類なので、100÷6=16.66で16～17回ほど「6」の目が出るのが普通です。
　25回も「6」の目を出すということは、不思議なサイコロと言っても良いのでしょうか。あるいは、今回たまたま「6」の目が出やすかっただけで、明日同じことを試したら違う結果になるのでしょうか。

　どちらとも言い切れず、非常に微妙なところと言えます。

　微妙なので、皆が納得できる何か一定の判断基準によって、これが偶然なのか、はたまた必然なのかを判断する必要があります。

　このときの判断基準となるのが「有意差」です。

　100回サイコロを振ったら「6」の目が25回出るサイコロがある。これは他の普通のサイコロと比べて、明らかに「6」の出る確率が高いものなのか、あるいは偶然の結果、誤差の範囲でしかないのか。

　これを統計学的な計算によって判定します。この判定によって「必然の結果」で生じたものだ、とされた場合、「有意差」あり、となります。
　その結果、このサイコロは「6」を出しやすい不思議なサイコロである、と初めて言えるようになります。

詳しい回答②：医学や薬学は、再現性のある科学である

　医学や薬学は、おまじないや宗教ではありません。

　その治療を行えば必ず効果がある（再現性がある）、と科学的に証明されていなければなりません。そのため、常にこの「有意差」の有無が必要になります。

　民間療法や健康食品が効能・効果をうたってはいけないのは、この再現性が証明されていないからです。つまり、ある人には効果があったとしても、それは偶然や他の要因によって得られた効果である可能性があり、他の人にも効果があるとは言えないのです。

グラフの差や数字の大小が問題ではない

　「有意差」があるかどうかと、グラフの見た目や数字の大小の差は関係ありません。統計学的な計算の結果、「有意差」があると判定されるかどうか、が問題です。
　　
　新薬Aは、血圧を5mmHgだけ低下させ、これが「有意差」であると証明された。
　新薬Bは、血圧を見かけ上40mmHgも低下させたが、その差は「有意差」であると証明されなかった。

　・・・というような結果が出たとき、薬の効果が認められるのはAだけです。Bの結果は偶然や誤差によるものなので、Bには効き目が無い、と判断されます。

　グラフの見た目や、数字の大小に惑わされないよう、きちんとデータを読み取る習慣をつける必要があります。

p<0.05とは

　有意差は、主に統計的な処理をした結果の「p値」によって設定します。

　ただし、p<0.05でなければ「有意差」と言えないというわけではなく、医学・薬学の慣習としてp<0.05が用いられているだけのものです。
　さらに精度の高い統計処理を行う場合にはp<0.001など、別の数字を使うこともあります。